Computer Vision 001 - Neural Radiance Fields

Introduction

Welcome to the first Computer Vision tutorial of my blog. While NeRF may be a bit advanced for a first post and not really a classical computer vision algorithm, I believe it is a great way to start off the series.

Neural Radiance Field, commonly known as NeRF, is a groundbreaking approach in the field of computer vision and graphics that was published in 2020. NeRF uses deep learning to synthesize novel views of 3D scenes, achieving photo-realisitc results that were previously unattainable with traditional methods. Moreover, follow-up works allow better performance or the ability to convert the network into a 3d model that can be used in application such as Blender. This blog post will overview the details of NeRF, explaining its core concepts, theory, and exploring its various applications. We’ll also have a demo at the end of the post to show give a hands-on example of what we’ll be discussing.

What is NeRF?

Let’s look at what the original ECCV 2020 Oral said about their method:

[NeRF is] a method that achieves state-of-the-art results for synthesizing novel views of complex scenes by optimizing an underlying continuous volumetric scene function using a sparse set of input views. Our algorithm represents a scene using a fully-connected (non-convolutional) deep network, whose input is a single continuous 5D coordinate (spatial location (x, y, z) and viewing direction (θ, φ)) and whose output is the volume density and view-dependent emitted radiance at that spatial location.

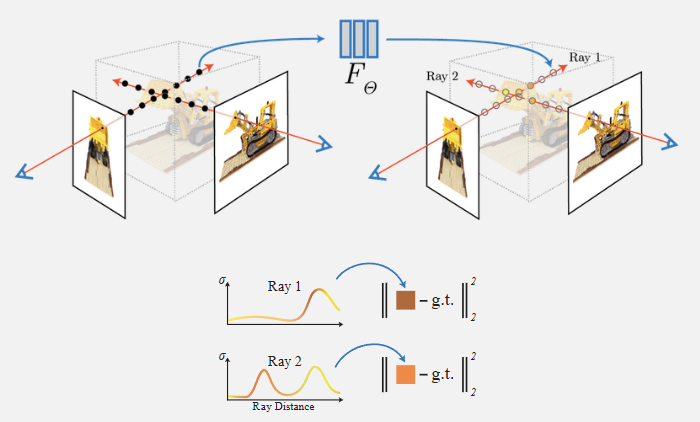
Let’s break this passage down. Essentially, NeRF allows us to query the RGB and volume density of a specific ray of light. The method takes in the viewing parameters of a “camera” in space from which beams of light are blasted into a scene. The key point of NeRF is that these beams of light “pass” through objects and don’t stop when hitting a surface; instead, each point in space carries some density that “absorbs” the light from the ray passing through it. From these rays of light, we can query the color and density of the scene at any point. In combination with a volumetric rendering algorithm, we can then render a 3D scene from any viewpoint.

NeRF Theory

If you are interested in reading the original paper, you can find it here.

Let’s dive into the theory of NeRF. As discussed before, the goal of NeRF is to represent a continuous scene as a 5D function that takes in a spatial location and viewing direction and outputs the volume density and view-dependent emitted radiance at that spatial location. This 5D function is represented by a fully connected neural network, which is trained using a set of input views of the scene.

Theory of the Volume Rendering Equation

Using this representation of a 5D neural radiance field, we can compute the color of a ray of light passing through the scene by using the following volume rendering equation:

\[C(r) = \int_{t_{near}}^{t_{far}} T(s) \alpha(r(s)) c(r(s), d) ds,\]

where:

• $C(r)$ is the color of the camera ray $r$
• $T(s)$ is the accumulated transmittance of the ray from $t_{near}$ to $s$
• $\alpha(s)$ is the volume density at point $s$, which the original paper interprets as the probability of the ray hitting an infinitesimal particle at point $r(s)$
• $c(r(s), d)$ is the color of the ray at point $r(s)$ and direction $d$
• $t_{near}$ and $t_{far}$ are the near and far bounds of the ray
• $r(s)$ is the point on the ray at distance $s$ from the camera
• $d$ is the direction of the ray

It is important to note that $T(s)$ can be written as $T(s) = \exp(-\int_{t_{near}}^{s} \alpha(s’) ds’)$, meaning that the more dense the points along the ray, the less light will pass through the ray at the current point. This is the key idea behind NeRF: the density of the scene at a point determines how much light passes through it.

However, in practice we can’t compute this integral exactly, as we only have a finite number of input views of a scene and each view is constrained by the number of pixels in the image. Instead, the original NeRF paper uses a stratisfied approximation to estimate $C(r)$. This approximation involves sampling points along the ray and computing the color at each point, then summing these colors to get an estimate of the integral. Specifically, this is done by splitting the ray into evenly spaced chunks and then drawing a random point in the chunk to estimate the color in that bin. By estimating the value of each chunk, we can estimate a continuous representation of the scene, allowing us (with other techniques) to compute the estimated color of a ray via:

\[\hat{C}(r) = \sum_{i=1}^{N} T_i c_i (1 - \exp(-\alpha_i \delta_i)),\]

where:

• $\hat{C}(r)$ is the estimated color of the camera ray $r$
• $T_i$ is the accumulated transmittance of the ray from the first bin to the $i-1$th bin, and is computed as $T_i = \prod_{j=1}^{i-1} \exp(-\alpha_j \delta_j)$
• $c_i$ is the color of the ray in the $i$th bin
• $\alpha_i$ is the volume density at the $i$th bin
• $\delta_i$ is the length of the $i$th bin ($\delta_i = t_{i+1} - t_{i}$)

This equation follows the same idea as the continuous version.

Positional Encoding

One of the key components of NeRF is the use of positional encoding to represent the 5D input to the neural network. The original NeRF paper uses a found that operating on only the x, y, z, $\theta$, and $\phi$ coordinates of the ray was not enough to capture the complexity of the scene. To address this, the paper uses a positional encoding to map the 5D input to a higher-dimensional space, allowing the network to learn more complex features of the scene. Specifically, the paper uses sines and cosines of varying frequencies to encode the input coordinates, which allows the network to learn high-frequency details in the scene. As discussed in the paper, this positional encoding is similar to the ones found in transformer tokens.

Hierarchical Volume Sampling

One optimization that the original NeRF paper makes is the use of two networks that the paper calls “coarse” and “fine”. The coarse network is used to estimate the volume density and view-dependent emitted radiance at a set of 3D points in the scene, while the fine network samples more from the dense portions of the coarse estimate. They do this by creating a probability density function from the normalized densities along the ray, which is then used to sample a new set of points. Both the old and new set of points are used as inputs for the fine network, allowing computationally effecient dense estimates in “important” areas of the scene while keeping some sampling in “unimportant” areas.

Applications of NeRF

In this section, we’ll discuss the various applications of NeRF.

3D Models

One application mentioned in the official NeRF project page is the creation of 3D meshes from the NeRF model. This is done by using a marching cubes algorithm to extract the surface of the scene from the volume density function learned by the NeRF model. This allows us to create 3D models of scenes that can be used in applications such as Blender or Unity. In my optinion, one of the best applications is NVIDIA’s Instant Neural Graphics Primitives, which provides an optimized training, inferences, and mesh creation pipeline for neural graphics models, including NeRF.

In terms of where I see NeRF being applied in business, I could see it being used in online stores where customers can view products in 3D before purchasing them. This would allow customers to see the product from all angles and get a better sense of what it looks like in real life. This could be especially useful for products that are difficult to visualize in 2D, such as furniture or clothing. In particular for complex furniture, one would be able to view specific parts of the furniture in 3D to get a better sense of how it looks, which would be better than an assortment of 2D images that may be taken at inoptimal angles.

Robotics

While I’m not the most knowledgeable in robotics, I found a few papers that discuss the use of NeRF in robotics. One paper, “3D Neural Scene Representations for Visuomotor Control” by Y. Li et al., uses a 3D scene representation from NeRF to control visuomotor tasks. From their paper, much of their applications involve fluids and the way they interact with rigid objects. This is an interesting direction for NeRF, and I hope to see future work in this direction.

Limitations

One of the main limitations of NeRF is its computational complexity. The original NeRF paper requires a large amount of memory and computation to train and render scenes. This is because the method requires a large number of input views to train the model, and the model itself is quite large (if you don’t use the miny version like we did in the demo). This makes it difficult to scale NeRF to larger scenes or more complex scenes. However, there have been several follow-up works that aim to address these limitations, such as Mip-NeRF.

Another limitation is training. NeRF requires a large number of input views to train the model effectively. This can be time-consuming and computationally expensive, especially for complex scenes. Additionally, the NeRF model, being a filly connected network, is shown to be slow at learning high frequency details in the scene. The follow-up work “Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains” addresses this issue by using a Fourier feature mapping to allow the network to learn high frequency details more efficiently.

One last limitation that I’d like to discuss is low-quality outputs when dealing with detailed scenes in the real world. This is because NeRF intrinsically struggles with scenes that have tiny details, complex lighting, or complex geometry. This is because the model is trained on a pseudo resolution based on the size of the “bins”, which may not capture all the details of the scene. This can result in low-quality outputs when rendering novel views of the scene. However, there have been several follow-up works that aim to address these limitations, such as Neuralangelo. This method uses 3D hash grids with multiple resolutions to capture the details of the scene more effectively. I plan on covering these follow-up works in future posts.

Demo

Now that the theory is out of the way, let’s dive in to the demo below. You’ll be able to run this on colab, though you may need a gpu to run this in a reasonable amount of time.

While I would love to implement the full NeRF algorithm in this demo, it would be too long to intuitively explain what each part of the code is doing (specifically on the hierarchical sampling). As such, I will be running and explaining my own version of mini-NeRF, which is a simplified version of NeRF that uses a smaller network and less input views. This will allow us to get a feel for how NeRF works without getting bogged down in the details.

You can find the colab notebook here.

Conclusion

I hope that this post did a good job explaining NeRF and its applications. The affects of NeRF in the computer vision space are very significant, as very important work in neural signed distance functions and 3D Gaussian Splatting have taken inspiration from NeRF. I hope to cover these topics in future posts, as well as other recent computer vision algorithms.

If you have any questions or comments, feel free to reach out to me on LinkedIn or via email. I hope you enjoyed this post and I hope to see you in the next one!